2024 05 12 HackerNews

2024-05-12 Hacker News Top Stories #

一句话摘要 #

Most of Europe is glowing pink under the aurora 极光在欧洲多地上空出现，从丹麦到澳大利亚墨尔本，人们观察到了白色、绿色、紫色、红色和橙色的极光，分享了使用AuroraWatch UK应用接收警报和拍摄极光的体验。

Immersive Math Immersive Math是一个交互式线性代数网站，提供丰富的内容和图表，帮助用户理解线性代数的概念和应用。

Thread: Tech we can’t use or teach? 文章讨论了Thread网络技术的应用，作者探索了低功耗电子学，并批评了Thread Group对非商业用户的限制。

Why the CORDIC algorithm lives rent-free in my head 文章详细介绍了CORDIC算法，这是一种在低功耗硬件上计算三角函数的算法，适用于嵌入式环境和性能较低的微控制器。

PeaZip: Open-source file compression and encryption software PeaZip是一个开源的文件压缩和加密软件，支持多种压缩格式，提供跨平台使用，并具有强大的加密功能。

One Minute Park “One Minute Park"是一个展示世界各地公园一分钟视频的项目，提供了一个宁静美丽的视觉体验。

The Emacs Window Management Almanac 文章探讨了Emacs中的窗口管理问题，提供了多种窗口管理方法和工具，以及提升窗口管理效率的建议。

Adam Curtis on the dangers of self-expression (2017) BBC记者Adam Curtis探讨了自我表达的复杂性，认为自我表达并非挑战权力和改变世界的有效手段。

Show HN: Wag, MFA and Enrollment for WireGuard “Wag"项目是一个为Wireguard VPN添加多因素认证、路由限制和设备注册功能的简单项目。

The derivative of a number (2014) 文章讨论了Edward Barbeau定义的自然数的导数概念，这是一个非线性操作符，最近的研究开始探索这一概念的潜在价值。

Most of Europe is glowing pink under the aurora #

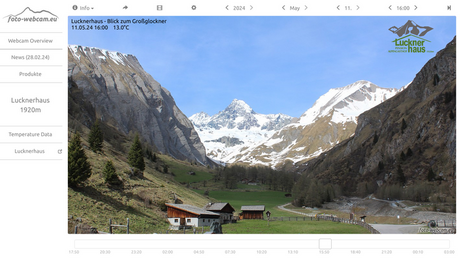
https://www.foto-webcam.eu/webcam/lucknerhaus/

这个网站是 Lucknerhaus Lucknerhaus（1920 米）的网络摄像头，提供对 Großglockner 山的景色。你可以观看实时视频，并查看当前的温度（4.0°C）。该摄像头每隔几个小时更新一次画面。如果你想观看实时视频，可以点击网站上的链接。

HN 评论 351 comments | 作者：luispa | 1 day ago #

https://news.ycombinator.com/item?id=40324179

在丹麦，观察到白色、绿色、紫色、红色和橙色的极光，令人惊叹美丽。
拍摄到极光的人分享体验，描述白色光柱形成交叉，延伸至整个天空，色彩丰富如闪烁的彩虹。
有人分享使用 AuroraWatch UK 应用接收到极光警报。
观察者表示照片难以捕捉到实际体验的规模和变化。
有人分享在北极圈，极光通常出现时间短暂，但有时持续数小时。
照片展示丹麦极光壮观景象。
观察者分享在葡萄牙家乡目睹极光，感受到微弱的红色光辉逐渐变化。
观察者在德国家乡拍摄到极光，描述整个天空闪耀着不同颜色和形态，令人难以置信。
观察者在荷兰东部看到类似云层的极光，拍摄了时间流逝的视频。
观察者在英国南部海岸拍摄到极光，描述看起来像淡淡的云彩，但有明显的绿色和粉红色。
观察者在法国南部看到极光，感受到首次极光体验的震撼。
观察者在澳大利亚墨尔本看到完整的极光，裸眼和相机均可见到多彩的光束和弧线。

Immersive Math #

http://immersivemath.com/ila/index.html

这个网站是关于交互式线性代数的内容，由 J. Ström、K. Åström 和 T. Akenine-Möller 合作编写。这本书是世界上第一本具有完全交互式图表的线性代数书籍。

内容包括导论、向量、点积、向量积、高斯消元、矩阵、行列式、秩、线性映射、特征值和特征向量等。网站提供了丰富的内容和交互式图表，帮助读者更好地理解线性代数的概念和应用。

HN 评论 33 comments | 作者：oumua_don17 | 8 hours ago #

https://news.ycombinator.com/item?id=40329388

感谢人们朝着这种模式发展。我对教科书和出版商心怀热切的憎恶。前者过时、静态、格式混乱，常常带有分散注意力的垃圾内容，或者更糟的是内联内容。这使得阅读变得比必要困难得多，带有可能跨越数页的不引人注目的旁注，很容易被卷入其中。虽然我理解它们有其用途，但并非人人都适用，因此拥有网页动态性的平台是我希望最终会朝着这个方向发展的。更不用说能够提供互动问题，快速反馈，而不需要翻页才能找出是否走在正确的道路上…而这种互动内容只是从简洁且难以解释的系统中提取意义的绝佳手段。
我希望这能为未来的教科书/出版物设立标准。除非我能够正确地将其可视化，否则我无法理解数学中的几个概念，而大多数现代教科书都使用了压缩严重且饱和度不足的 JPG。
这看起来像是教育的未来。特别是配合虚拟现实。
我希望看到这种方法应用在几何代数，即 Clifford 代数上。
爱这个 bootstrap 3。简洁，有效，并符合最少惊讶原则。
这看起来令人难以置信！现在唯一需要的是在背后加入一些对话式人工智能魔法，根据学生的简单问题进行内容过滤和调节，然后就可以开始了。请注意，这是在 2019 年完成的，所以现在是将其完善并扩展到数学的其他领域的绝佳时机！假设这是 ThreeJS，你可以为模拟制定一个开源文件格式，甚至将其应用于现有流行数学教科书的众包应用程序，按照图表/页码。我的意思是，线性代数很酷，但优质免费几何教育的市场是无限的。是否有大牌数学教育提供模拟，还是仍然只有动画/图像/视频？
看到有人建议在这样的书籍中添加人工智能真是让我痛心。当前的人工智能在数学方面臭名昭著。我们最不需要的是 ChatGPT 弄错减号并混淆读者，或者使他们的理解倒退数周。

Thread: Tech we can’t use or teach? #

https://overengineer.dev/blog/2024/05/10/thread/

这篇文章是由 Dennis Schubert 撰写的，讨论了他在项目中遇到的技术问题以及对 Thread 技术的探索。文章开始介绍了他之前开发的过度工程化的咖啡豆存储和库存管理解决方案，以及如何通过对显示屏固件进行软件调整，将电池续航时间从 40 天提升到 55 天。

随后，他开始探索低功耗电子学，发现 WiFi 对于这类项目来说效率不高，因此转向寻找替代方案。文章介绍了 Thread 网络技术，基于 6LoWPAN 和 IPv6，可以连接到家庭网络，提供了一种更高效的选择。

然而，作者也指出了 Thread Group 对于非商业用户的限制，需要支付昂贵的会员费才能合法使用 Thread 技术。文章最后批评了 Thread Group 对于非商业项目的限制，认为这种做法不利于技术的普及和创新。

HN 评论 125 comments | 作者：todsacerdoti | 19 hours ago #

https://news.ycombinator.com/item?id=40326269

LoRaWAN 被城市采用是因为在法律方面较简单，但与丹麦电信法相关的限制给了电信公司一种垄断高速“互联网”的权力，对于 Thread 也适用。
Threads 永远不会扩展到那个程度吗？它的用例完全不同于 Threads 的设计目的吗？
如果您是一个没有能力加入 Thread Group 的业余爱好者，没有合法使用 Thread 的途径吗？
专利不适用于私人试验除非涉及商业活动，但专利法并未排除私人使用。
欧洲的软件专利理论上不被授予，但版权法仍然适用，他们可以基于版权法删除引用规范的内容。
您可以因任何事情而被起诉，无论其是否违法。诉讼是法院决定您的个人情况是否非法的过程。
有可能私下使用 Thread，但需要谨慎，因为该协议设计了防止与“假”设备交互的机制。
Thread 的许可协议旨在防止与“假”设备交互。您的设备需要提供特殊的加密证书才能正常工作。
Thread 的许可协议似乎是为了防止对现有基础设施进行非法使用，这可能会导致该技术被有效合法化。
Thread 协议的法律术语旨在防止破坏现状，以保护最大科技公司的财富。

Why the CORDIC algorithm lives rent-free in my head #

https://github.com/francisrstokes/githublog/blob/main/2024/5/10/cordic.md

这篇文章介绍了 CORDIC 算法，它是一种用于在低功耗硬件上计算三角函数（如 sin、cos、tan 等）的算法，而无需使用浮点运算单元（FPU）或昂贵的查找表。CORDIC 算法将这些复杂函数简化为简单的加法和位移操作。

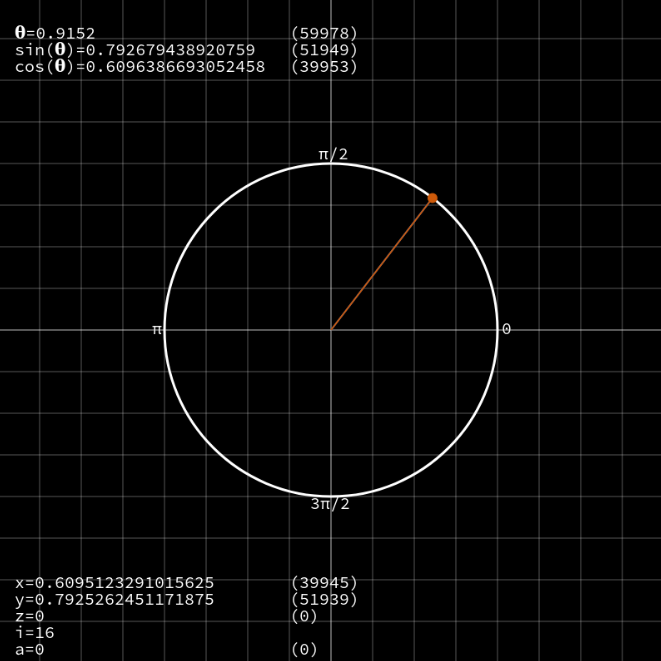
文章详细解释了算法的工作原理，包括向量数学、三角学、收敛证明和一些巧妙的计算机科学方法。作者强调了这种算法的简洁性和优雅性，以及其在嵌入式环境中的应用，特别适用于性能较低的微控制器和 FPGA。文章还讨论了如何避免使用浮点数表示有理数，介绍了固定点表示法的概念和实现方法。

此外，文章深入探讨了 CORDIC 算法的实现细节，包括如何通过旋转向量来逼近各种三角函数值，以及如何利用位移和加法操作来实现这一过程。文章还提到了如何通过预计算表格和特定角度的选择来优化算法，以实现更高效的计算。

HN 评论 48 comments | 作者：todsacerdoti | 18 hours ago #

https://news.ycombinator.com/item?id=40326563

作者提到 CORDIC 算法在 FPGA 等领域有应用，也可用于游戏开发中的固定点物理引擎；
x87 存在问题，需确保舍入模式等设置一致；
IEEE-754（2008）规范明确，建议避免 x87，现代处理器内置 FMA；
编译器可能重新组织表达式，对于小型程序和自编库，确保避免这些问题较为直接但繁琐；
LLVM 尝试对各种三角函数进行常量折叠，IEEE-754 规范建议正确舍入结果；
固定点在游戏开发中曾流行，主要出于性能考虑；
CORDIC 可用于多种操作，如对数、指数、平方根、向量旋转等；
CORDIC 操作可通过四元数更高效地执行；
CORDIC 可扩展到任意 Lie 群；
CORDIC 在高中学习中替代了 Taylor 级数，用于计算三角函数；
一些现代 MCU 具有硬件 CORDIC 外设，用于固定点计算，避免浮点精度损失；
CORDIC 在 DSP 领域曾流行；
CORDIC 可节省设计空间，查找表与插值更快；
神经网络通常不使用三角函数或复数；
CORDIC 可计算超越三角函数，但在 ML 中不太实用；
“住在我脑海中免费”是一个陈词滥调，描述强迫性思维；
租金在此处指维持某知识的努力，易于回忆；
该短语通常描述强迫性、侵入性思维；
一些人将其解释为应该放下并忘记的事物；
该短语通常用于描述政客对不喜欢的政治家的关注。

PeaZip: Open-source file compression and encryption software #

https://peazip.github.io/

https://peazip.github.io/ 是 PeaZip 免费文件压缩工具的官方网站。PeaZip 是一款类似于 WinRar、WinZip 和 7-Zip 的免费文件压缩工具，基于 7-Zip / p7zip 压缩器、Facebook Zstandard 压缩器、FreeArc、Google Brotli 压缩器、PAQ 压缩器系列、PEA（归档和加密）项目等开源技术。

PeaZip 致力于提供其他同类应用程序常被忽视的功能，如桥接 GUI 和 CLI 应用程序，提供两因素身份验证（密码 + 密钥文件）以增强安全性，支持不常见的压缩格式等。该工具跨平台支持 Linux、macOS 和 Windows 系统，提供 200 多种存档格式的支持，强大的加密功能，以及易于导出 GUI 任务为命令行脚本等特性。

PeaZip 是自由软件，采用 GNU LGPLv3 许可，安全可靠，不收集用户数据。用户可以从 GitHub 和 Sourceforge 等官方仓库下载 PeaZip。

HN 评论 69 comments | 作者：thunderbong | 13 hours ago #

https://news.ycombinator.com/item?id=40327631

PeaZip 是优秀的软件，使用 Lazarus 编写并用 Free Pascal 编译，推荐尝试体验高质量软件可通过非主流工具构建。
开发者眼部手术后可能无法继续开发，但看起来情况良好。
从应用程序拖放到系统对用户体验提升很大，但实现并不简单，许多开发者选择 Electron。
许多 DE 使用相同标准，所以不支持 Linux 的开发者选择不支持 Linux。
GID（通用图像解码器）用 Ada 编写，在某些基准测试中明显优于 ImageMagick（用 C 编写）。
喜欢看到使用 Free Pascal 编写的软件，它们往往体积小且高效。
PeaZip 是 Lazarus 能力的最佳示例，激发了 Pascal 爱好者的灵感。
7-zip 和 PeaZip 都具有一个不寻常的功能：能够浏览 Windows Explorer 拒绝加载的 NT 路径。
在 Linux 下使用 PeaZip，因为它能够提取 OneDrive 生成的大型损坏 zip 文件。
PeaZip 不支持在 UI 中带引号（"）的密码，可能存在安全问题。
PeaZip 与 7zip 相比，具有更好、更方便的 GUI（和工作流/行为）。

One Minute Park #

https://oneminutepark.tv/

“One Minute Park”，展示一分钟世界各地的公园的视频，景色美丽，让人沉静。

HN 评论 21 comments | 作者：cookingoils | 1 day ago #

https://news.ycombinator.com/item?id=40323785

观看视频时关闭声音更具沉浸感，自然环境的宁静与周围声音融合，画面更生动。
在温暖的夏日室内观看公园视频感到不安。
建议添加按钮启动播放，以适应视频和音频自动播放禁用的用户。
视频收藏，感谢分享。
对德国严格的隐私法律提出疑问，是否需要获得视频中所有人的同意。
在德国拍摄街景是否需要每个人的许可，实际上只要人物非焦点，背景即可。
迪士尼乐园在 90 年代告知拍摄情况，可能缓解许多情况。
视频让人立即平静下来。
视频背景音乐愉悦，适合工作时放置背景。
想象立体录制并在 VR 头戴设备上观看，适合冬季。
视频看起来像 AI 生成，但实际包含太多细节。
视频制作甜蜜可爱。
类似 window-swap.com 的体验。
制作者通过“一分钟”概念使内容易于创作和管理。
希望视频中有更多狗，更多狗海滩场景。

The Emacs Window Management Almanac #

https://karthinks.com/software/emacs-window-management-almanac/

这篇名为《The Emacs Window Management Almanac》的文章探讨了 Emacs 中的窗口管理。文章指出 Emacs 的窗口管理因其非常灵活和细粒度的布局系统与粗糙的控制相结合而备受诟病。作者总结了多种窗口管理方法，包括基本的其他窗口切换体验、使用 windmove 库进行窗口选择和交换、使用 winum 库进行窗口编号和选择、以及使用 ace-window 库进行更高级的窗口操作。

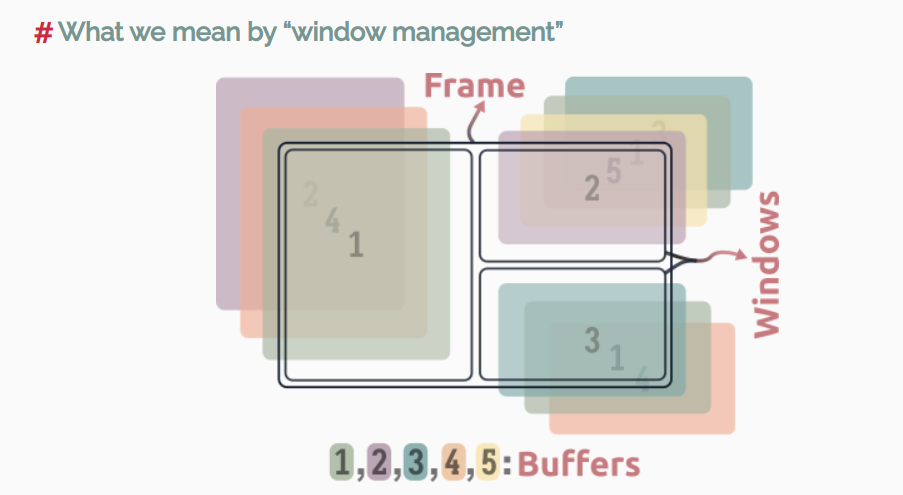
此外，文章还介绍了如何通过键盘驱动的方法、Avy 工具和其他方式来改善窗口管理体验。作者还提到了一些窗口管理的技巧和工具，如 scroll-other-window 和 isearch-other-window，以便更高效地在不同窗口间切换和执行操作。整体而言，这篇文章提供了丰富的窗口管理资源和建议，适用于想要提升 Emacs 窗口管理效率的用户。

HN 评论 29 comments | 作者：dargscisyhp | 19 hours ago #

https://news.ycombinator.com/item?id=40326362

该帖子中有关 Emacs 窗口管理的评论观点包括：golden-ratio 和 zoom-mode 是调整窗口大小的推荐工具；
有人喜欢将窗口分为 70% 和 30% 的比例；
有人认为使用 frames-only-mode 和 ace-window 会提高效率；
也有人喜欢使用 EXWM 或 StumpWM 来管理窗口；
另外，有人提到了 zygospore 这个补充包。

Adam Curtis on the dangers of self-expression (2017) #

https://thecreativeindependent.com/people/adam-curtis-on-the-dangers-of-self-expression/

在这篇名为“Adam Curtis on the Dangers of Self-Expression” 的文章中，BBC 记者和纪录片制作人亚当·柯蒂斯（Adam Curtis）探讨了艺术、个人主义、权力、神话以及自我表达的复杂性。

艺术：文章提到艺术是一种很好的方式来描述世界和时代的情绪，但自我表达并不是替代政治行动来改变世界和挑战权力的手段。从 20 世纪 70 年代初开始，自我表达被视为新的政治方式，但柯蒂斯认为这并非挑战世界中不良现象的有效途径，因为整个世界实际上是建立在自我表达的基础上的。
个人主义：现代自我表达的历史可以追溯到嬉皮士时代。柯蒂斯认为，当左翼运动在 60 年代末 70 年代初崩溃时，人们开始将注意力转向自我表达，作为对左翼失败的替代方式。然而，他指出，即使艺术作品传达着激进的信息，如果批评是通过自我表达实现的，实际上是在滋养他们试图推翻的权力结构。
权力：柯蒂斯认为，要让世界变得更美好，必须从权力所在开始。他指出，我们生活在一个认为自己是独立个体的世界中，很难看到集体力量。他提到，计算机能够看到我们作为一个群体的相似之处，但我们被鼓励只关注自己，而不是看到自己作为整体的一部分。
神话：柯蒂斯谈到了对魏伯（Max Weber）的引用，预言我们将进入一个官僚化时代，失去了神秘和令人着迷的感觉。他认为，阴谋论可能是试图以扭曲的方式重新赋予世界神秘感的尝试。他认为，资本主义的衰落意味着需要一种新的神话形式来重新赋予世界魅力。

这篇文章涵盖了柯蒂斯对自我表达的看法，以及他对艺术、个人主义、权力和神话的深入见解。

HN 评论 83 comments | 作者：greenie_beans | 23 hours ago #

https://news.ycombinator.com/item?id=40325542

当代艺术世界被认为是一个巨大的个体集合，表达方式符合画廊、博物馆、拍卖等市场体系，缺乏任何中心理念或理想。
现代艺术世界主要是为了以税收优势的方式购买低成本材料而设计的逃税和敲诈计划。
现代艺术世界主要是为了将资产转移至国家和国际法律影响之外而设计的逃税和敲诈计划。

Show HN: Wag, MFA and Enrollment for WireGuard #

https://github.com/NHAS/wag

这个 GitHub 地址（ https://github.com/NHAS/wag）包含一个名为"Wag"的项目，它是一个简单的 Wireguard 2FA 项目。该项目的主要功能包括：

定义需要 MFA 授权的路由或公共可访问路由
注册新客户端的简单 API
高可用性
多种 MFA 选项，包括 webauthn、oidc 等
需要安装 iptables 和 libpam
需要以 root 身份运行
需要在 sysctl 中启用转发
不需要 wg-quick 或其他等效工具，只要内核支持 Wireguard

该项目提供了设置说明，包括二进制发布和源代码构建的步骤。管理 wag 服务器的命令包括启动、清理、重新加载 ACL 等。此外，还提供了用户指南、配置文件参考以及 ACL 规则定义等详细信息。

“Wag"项目的目标是为 Wireguard VPN 添加 MFA、路由限制和设备注册功能。

HN 评论 32 comments | 作者：Nullence | 17 hours ago #

https://news.ycombinator.com/item?id=40326615

注册过程中服务器生成私钥发送给客户端，而不是客户端生成私钥发送公钥给服务器，建议使用 https 替换 http；
用户认证需要浏览服务器 VPN 地址，会提示输入 2FA 代码，但客户端如何意识到会话超时？希望有类似 WiFi 上的强制门户检测功能；
WireGuard 密钥是永久会话密钥，是否考虑实现会话管理？建议使用 Firezone 进行会话管理；
版本 1.0 在每个认证会话中旋转 WireGuard 密钥，私钥永远不会离开隧道进程内存，需要 Firezone 客户端支持；
建议构建 VPN 客户端时使用 WG，具有每个客户端的永久认证密钥，用于建立初始隧道到 VPN 控制器，然后获得另一个会话密钥；
是否保护 TOTP 代码的暴力破解？建议增加速率限制或重试次数限制；
TOTP 检查可防止被盗笔记本中的凭据泄露，密码管理器更易泄露；
MFA 旨在防止泄露影响服务，并通知用户/管理员，但如果能在 60 秒窗口内强制使用 TOTP，则 TOTP 将无效；
网站选择 WireGuard 应该有更现代化的设置，可能会大量使用（自助）ULA。

The derivative of a number (2014) #

https://rjlipton.com/2014/08/19/the-derivative-of-a-number/

这篇文章讨论了 Edward Barbeau 在 1961 年定义的一个关于自然数的导数概念。文章介绍了 Barbeau 的导数定义规则，其中对于所有质数，导数为该质数的幂次减一；对于所有数，导数为该数的因子之和。

Barbeau 的导数概念并非线性操作符，且导数的计算并不像通常的导数那样简单。文章提到 Barbeau 的导数概念虽然有趣，但似乎并未受到深入研究。最近有一些关于这一概念的论文出现，可能研究人员开始意识到这一概念中可能隐藏着一些价值。

这些论文主要探讨了导数的内在性质和增长规律，以及如何将这一概念扩展到更广泛的数域。文章还提到了一些相关研究论文，并探讨了如何利用这一概念解决数论中的开放性问题。

HN 评论 74 comments | 作者：tempodox | 19 hours ago #

https://news.ycombinator.com/item?id=40326305

数学家喜欢称呼具有相同“结构”的两个事物为相同的名称，即使它们在其他方面并非明显相关。在这种情况下，共享的结构是函数的导数和 D(n)都遵循导数的乘法法则，这意味着它们在某种程度上是相同的对象。
类别理论等领域允许人们“放大”到足够抽象的程度，使两个看似不同的概念实际上是应用于不同背景的相同概念。
对于抽象代数中的导数，它被称为“导出”，满足两个属性：1）它是线性的；2）它满足乘法法则。任何满足这些规则的函数通常被称为“导数”。
对于整数上的 D(n)函数，为什么称其为导数？它与微积分导数的概念几乎没有概念上的相似性。
对于多项式，Leibniz 法则保证 D 与标准导数一致，这也是一个很好的合理性检查。
D(n)函数在整数上可能很有趣，但为什么称其为导数？为什么不起一个不同的名字？
对于整数的 D(n)函数，它只依赖于数字的质因数分解中指数的多重集，这使得它类似于除数计数函数、omega 和 Omega 函数、莫比乌斯函数等。
对于多项式，D(x+a)=1，其他通过乘法法则计算，这与微积分中的导数定义完全相同。
对于整数，D(x+a)=1，其他通过乘法法则计算，这与微积分中的导数定义完全相同。